Letter number 71 of January 2013
- TOPIC
- STATISTICS
- RESEARCH
- QUESTIONS & COMMENTS
- NEW
News : The risk-free rate the time for change is now!
Given the current state of the art, we are unable to work out the cost of equity and the cost of capital unless we can estimate the risk-free rate. The CAPM postulates that the rate of return that should be required of an asset is the risk free rate plus a risk premium that is proportional to the risk of the market of the asset in question: Rf + β x [E(Rm) - Rf] (1) . Alternative models to the CAPM, such as the APT, also require a risk-free rate.
What is a risk-free rate?
In order to estimate the risk-free rate, the government bond rate over the most frequently issued or negotiated period is often used - 10 years in France for the OAT or in Germany for the Bund, and 30 years in the USA. The justification given is that this long-term period is around the same length as that of the average cash flow of a share or of capital employed, which will necessarily also be long-term.
For their part, the researchers who designed the CAPM did not provide a concrete definition of the risk-free rate, except to indicate that it is an asset for which the standard deviation of possible returns is zero. This is an excellent definition of a risk-free asset. Because it is risk-free, its return is certain and the standard deviation of its possible returns is zero since there is only one possible return.
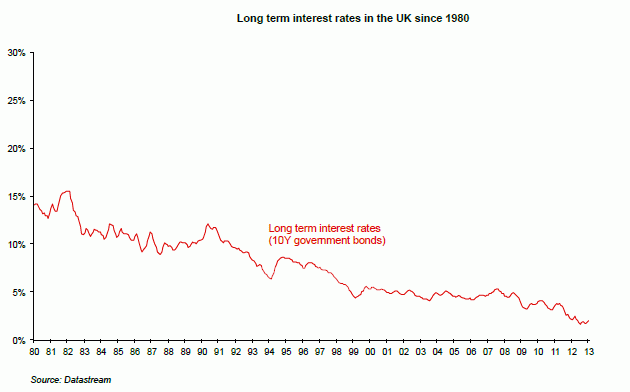
It is obvious that a 10- or 30-year government bond is not a risk free asset. Its value may fluctuate over the course of time in line with changes in interest rates, and since it has been issued over a long period, such changes are inevitable, as can be seen from the graph below showing the yield-to-maturity of UK 10-year bonds since 1980:
Even investors who intend to hold onto their government bonds until they reach maturity, and for whom the risk of fluctuation in the value of capital is irrelevant, are concerned by these fluctuations in interest rates. They remain exposed to the risk of reinvestment of coupons. As a matter of fact if at the issue date the yield to maturity announced was, for example, 4%, this rate can only be achieved if the coupons are on average, reinvested at this rate of 4% (and if the bonds are kept until maturity).
Additionally, unexpected changes in inflation could have a negative impact on what had appeared to be a risk-free investment. It is true that for around 30 years, inflation levels have been lower than expected, but this situation will not last forever, as our more senior readers will know, those who lived through two decades of rising inflation in the 1960s and 1970s.
Finally, there is a risk of the solvency of the issue, which the increasing debt of most western counties means is not merely a theoretical possibility, as current events over the past two years and a half have demonstrated.
Although the risk of reinvesting coupons and that of inflation can be combated through the use of zero coupon bonds and bonds indexed to inflation, the risk of solvency is more difficult to neutralise. There are, of course, CDSs, but until they are offset by a clearing house(2), those buying this sort of protection run the risk that whoever sold it to them, may default. Moreover, unlike the government bond market, the CDS market is opaque and its liquidity is doubtful.
So what is to be done?
So it seems to us, now that the solvency of governments is not such a sure thing as it was in the past, that it would be a good idea to take another look at the choice of the risk-free rate. It should be very clear to our readers that the CAPM formula is only internally accurate because the risk-free rate is effectively risk-free. If not, this model should not be used. But since there are no other models that can be used, there’s not much choice. . .
We see no other option but to take a short-term interest rate, since over the short term, fluctuations in interest rates and inflation are a lot lower, even negligible, as the risk of reinvesting coupons doesn’t exist. If we take a 1- to 3-month Treasury Bill of a government rated AAA, the solvency risk is de facto, zero.
This view, which goes against majority practice in Europe, is not as iconoclastic as all that. The three main worldwide suppliers of risk premiums on the equity markets, Ibbotson, Marsh Dimson and Associés en Finance, offer users equity market risk premiums that are calculated on the basis of long-term rates, and on the basis of short-term rates. Obviously, the most important thing is not to add to a short-term rate, a risk premium calculated using a long-term risk-free rate, or vice versa.
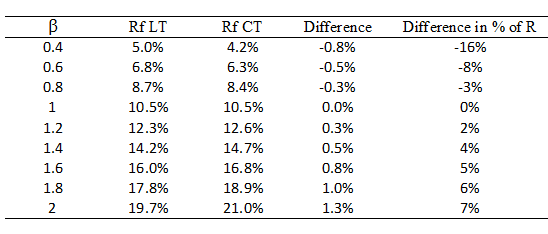
In the great majority of cases, the change that involves moving, for the risk-free rate, from a long term-rate which is in fact risky in contradiction with what it should be, to a short-term rate, which is really without risk, has a low impact on the discount rate because of the current low slope of the interest rate curve. Only shares with a very low β are significantly impacted. But firms with a β of less than 0.5 are few and far between, for example, less than 0.5% of the sample taken by Associés en Finance.
Required rate of return on a share on the basis of its β for a short-term interest rate of 0.05% and a 10-year rate of 1.35% (German data) and a market rate of return of 10.5% (data from mid December 2012):
We might well be sorry that future cash flows are no longer discounted using a long-term rate (risk-free rate + risk premium), with a similar duration as the one of cash flows. This seems to us to be an optical illusion. In fact, cash flows are discounted at Rf + β x [E(Rm) - Rf], i.e., on average (β de 1), at E(Rm), which is a long-term rate since is equalises the market value of today with the present value of future cash flows generated. By adding a premium to a short term rate, we no longer have a short-term rate. In order to convince any latter-day doubting Thomases, we can easily present the CAPM formula: Rf + β x [E(Rm) - Rf] as: E(Rm) + (β – 1) x [E(Rm) - Rf] where we find a premium (β – 1) x [E(Rm) - Rf] which is added to a long-term interest rate: E(Rm), and this whether the interest rate Rf used is a short-term or a long-term rate.
We might also wonder how, with a risk-free rate equal to the rate of 3-month German Treasury Bills for the euro zone, we take into account the risk of certain countries within the euro zone (Spain, Italy, Greece, etc.). Today, we add a spread to the long-term German rate used, which comes from the CDS market or the countries’ borrowing, but its current extent often creates a problem. Some values have thus decided to take a medium spread, calculated over a more or less long period, or to take the ideas that the spread must, sooner or later, return to a historic average, and to use a technique for fading(3) this spread in the future. All of this makes sense, but opens a lot of possibilities between which it is difficult to choose objectively - length of the fading period, speed of return to the average, calculation period of the average, etc. , while they have a major impact on the value calculated.
With a short-term interest rate as the risk-free rate, all of this is of no use as soon as the beta ratio is calculated against a European index and not a national index. For example, the β of an Italian company, calculated against the Milan stock exchange, is significantly lower than what it would be if calculated against a European index. In a recent case, we obtained for the β of an Italian company calculated against the Milan stock exchange, a figure of 0.43, but when we calculated it against the European index, we arrived at 0.63. This is because the Italian market is more volatile than the European market take as a whole. It’s a bit like taking an aircraft that’s flying at 850km per hour and a passenger is walking down the aisle. Seen from the aircraft, the passenger is walking at 2km/hour, but seen from the ground, he’s walking at 852km/hour.
In other words, the country risk is integrated into the β and doesn’t need to be taken into account anywhere else if it is correctly calculated against a European index, and not against a local index. Since in any event, the beta has to be calculated, we thus avoid debatable choices when taking into account the country risk within the euro zone.
But why change now?
Fundamentally, because having seen a year ago CDSs exceeding 100 base points for the German bund and 200 base points for French OATs with the same maturity, it is no longer reasonably possible to carry on as if these government bonds were still risk-free products. And this even though these CDS have dropped to 30 and 80 bp respectively. We were already closing our eyes to interest rate fluctuations and forgetting about inflation since it had stabilised at a low rate a very long time ago. But the risk of solvency put at at least 10% of the discount rate (a CDS of 80 base points for France with a cost of capital of 8 to 9% on average), cannot be ignored. Enough is enough!
We’ve been thinking about it for quite a long time. The results of a survey that we conducted on this subject in the second half of 2012, available on the home page of the site www.vernimmen.com, have confirmed our choice. Of the 967 respondents, 49% chose a short-term interest rate and not a long-term rate like the risk-free rate.
WHAT IS A RISK FREE RATE FOR YOU?
Votes %
| Votes | % | |
| A long term government bond | 97 | 10% |
| A long term government bond with an AAA rating | 351 | 36% |
| A corporate bond with an AAA rating | 44 | 5% |
| A treasury bill issued by a AAA rated government | 355 | 37% |
| A short term interest rate like Eonia, Euribor or Libor | 120 | 12% |
Total answers : 967
We were expecting a much lower figure. All of this makes us think that “change, it’s now”, for the risk-free rate too.
From now on, we’ll be using as the risk-free rate in the euro zone, the rate of 1-month German Treasury Bills and in the dollar zone the rate of 1-month US Treasury Bills.
1) For further details, see chapter 19 of the Vernimmen
2) For further details, see chapter 49 of the Vernimmen
3) For further details,see chapter 32 of the Vernimmen
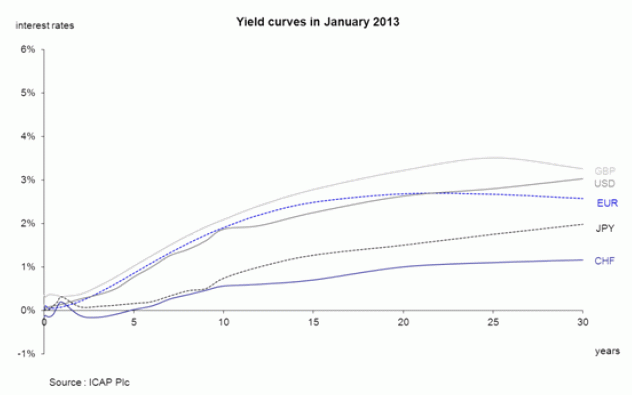
Statistics : Interest rate yield curves
One might have the impression that interest yield curve slopes are upward, meaning that investors are expecting an increase in interest rates . But when you glance at the scale of this graph you realized that this is an illusion. In all major currencies, government bonds are yielding less than 1% (before tax for investors) for maturity up to 5 years. This has never been seen before.
Research : Bond yields and economic disasters
With Simon Gueguen – Lecturer-researcher at the University of Paris Dauphine
The renowned American macro-economist and Harvard professor, Robert Barro, qualifies as “economic disasters”, situations in which the GDP of a country falls by more than 10%1. According to this criteria, OECD countries experienced 58 economic disasters during the 20th century, with almost all of them occurring during the first half of the century2. Barro shows how these events, although rare in recent history, could help to explain the valuation of financial assets. Taking up this idea, Gavyn Davies3 published an article that explains historically low bond yields on his Financial Times blog. He bases his findings on research4 published by Fulcrum Asset Management, the investment fund he chairs.
On the basis of the 10% criteria, since 2007, Ireland, Iceland and Greece have experienced economic disaster. Other countries may follow, particularly in the event of a break-up of the euro zone. Such disasters impact on household revenues (and thus consumption), and at the same time the flows generated by shares. If this risk increases, the value of shares should fall.
The central idea of the article is as follows: even if the risk of default on government bonds increases slightly, investors may resort to them to protect themselves against risks weighing on shares. Consequently, the government bond yield rate may fall when the default risk has increased. This is the case in Germany – while the probability of default implicit in Germany debt went from 0.5% in early 2010 to close to 2%5 in 2012, government bonds are negatively correlated to shares and their yield rate has dropped.
However, when the risk of default becomes too great, government bonds no longer fulfill the function of refuge security. The correlation to shares can become positive. The yield rate then increases sharply – this was the case for Spain and Italy. Empirically, Brookes and Daoud note that an implicit default risk of 3% constitutes the tipping point. Below that, government bonds provide assurance on the economy, and the yields required may reduce when risks increase. Above that, the correlation with shares becomes positive and assurance is no longer an issue; yield rates increase sharply.
This article suggests an explanation for two current phenomena:
- the persistence of very low yield rates for government bonds on which the risk of default has, however, increased;
- a sharp increase in yield rates when default risks are too great and the correlation between shares and government bonds becomes positive.
1 See for example R. BARRO and J. URSUA (2008), Macroeconomic Crises since 1870, Brookings papers on Economic Activity, pages 255-335.
2 The two exceptions are Iceland in the 1980s and Finland in the 1990s
3 Gavyn Davies was a partner at Goldman Sachs and then Chairman of the BBC. Today he is Chairman of Fulcrum Asset Management.
4 M. BROOKES and Z. DAOUD (2012), Disastrous bond yields, Fulcrum research Paper
5 These default probabilities are measured using spreads on CDSs (credit default swaps).
Q&A : Why have UK pension funds modified the composition of their asset portfolios?
For the first time since the 1950s, the share of bonds in the asset portfolios of UK pension funds is larger than that of shares – 43.2% compared with 38.5% according to statistics kept by the British regulator.
There are several reasons for this.
With a large number of baby boomers reaching retirement age, and the numbers of workers just behind them being much lower, the average retirement commitment of pension funds is becoming shorter. It is thus logical for pension fund managers to reduce this risk of their portfolios in order to be able to cope with larger and closer payouts of cash. This means that they have increased the share of bonds at the expense of shares in their portfolios.
Since 1998, the performance of shares has, on average, been disappointing to say the least, with 3.4% of dividends reinvested. On the other hand, the performance of bonds has been outstanding, thanks to the drop in rates. When bonds had to be sold before their maturity dates, capital gains were made. When they were kept until they matured, the rate of return obtained was more or less that which had been announced at the issue, so positive, and higher than the current rate. After a while, the past performance, and especially its resistance, even if it is no guarantee of the future performance, ends up becoming a reference and one would really have to have a huge amount of faith in investing in shares, in order to resist the lure of the bond market.
A fund manager who is seeking a bit of risk, and thus slightly higher returns, no longer needs to go onto the equities market to find it. The enlargement of the bond market, thanks to the development of corporate bonds, not to mention the high yield compartment, will provide what fund managers are looking for.
Given the extent of the funds managed by UK pension funds (£800bn), the composition of their aggregate portfolios tends to stick close to the financial assets available as a means of investment. The fall in share prices since 2000, share buybacks and delistings that exceed the amount of share issues and IPOs that are becoming increasingly rare, the strong return to bond issues by governments since 2008 and the more frequent recourse to the bond market by companies, have all developed the relative share of listed debt at the expense of that of equity.
Questions may however be raised as to the relevance of this choice, bearing in mind that the current nominal rates of government bonds of the large bond issuing countries (the USA, UK, German, France, Japan) have fallen to below the rate of inflation, and that inflation, after 30 years of falling on a practically continuous basis, could well, at any time, start rising again. And when we know that investing in shares has not historically provided good protection against inflation, we might spare a thought for British pensioners who will be retiring within the next 10 or 20 years.
New : REVIEW OF A BOOK: Corporate Financial Risk Management
The Handbook of corporate financial risk management by Stanley Myint and Fabrice Famery, Risk books, 2012
This is a book which is fulfilling a long-standing and deep gap in existing literature : How should industrial companies manage their financial risks. While there are many books devoted to the risk management for banks and financial companies, very little is written on the subject of corporate financial risks, and it is mostly written by academics and not practitioners. In contrast, the authors of this volume have spent seven years working with 350 Treasurers and CFOs of largest European companies (including many in Italy), and now present their results in the form of 31 practical, rigorous and detailed case studies, covering all the main areas of financial risk management: from currency and interest risk to commodity and counterparty risks. Funding and M&A situations are also presented. Any Treasurer, CFO, Financial Director or other financial professionals would benefit from reading these company stories as they can easily be adjusted to any company situation.
For more details see: www.riskbooks.com/corprisk
Readers of Vernimmen can get the 25% discount by entering VERNIMMEN25 in the promotional code area that is present in the basket page of Riskbooks.com. Or they can email books@incisivemedia.com quoting VERNIMMEN25 and get the discount.