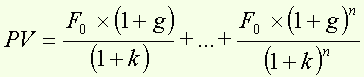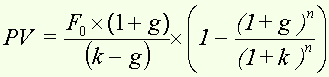Then we have :
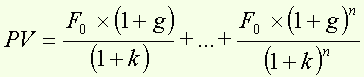
or :
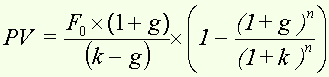
assuming that k > g
Thus, a security that pays out 0.8 the first year, growing by 10% for the four following years has, at a discounting rate of 20%, a present value of :
PV = (0,8/0,1) ´ (1 - (1,10/1,20)5) = 2,82
| Present value of an annuity that grows at rate g for n years |
Around the formula...
We assume that F0 x (1+g) is the
first year cash flow and grows at rate g over n years.
Then we have :
or :
assuming that k > g
Thus, a security that pays out 0.8 the first year, growing by 10% for the four
following years has, at a discounting rate of 20%, a present value of :
PV = (0,8/0,1) ´ (1 - (1,10/1,20)5) =
2,82